
7.1) estimates the degree of the linear relationship.
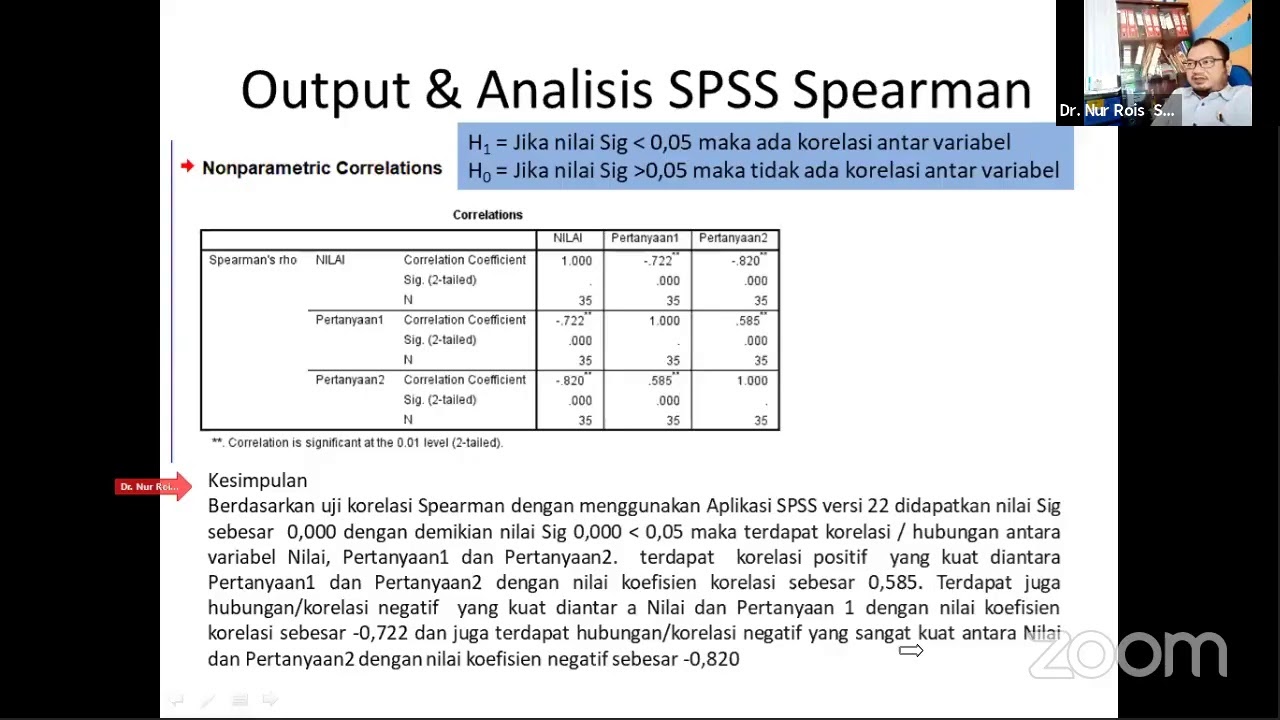
KORELASI SERIAL DENGAN SPSS SERIES
Using a bivariate time series sample, \(\left \\), this measure allows to study the relationship between two climate variables, each described by its own climate equation (Eq. The correlation measures how strong a coupling is between the noise components of two processes, X The results of this study suggest that musical training or signal processing strategies that improve F0 discrimination should improve consonant identification in fluctuating noise. The strongest correlations were observed for measures of complex tone F0 discrimination with phoneme identification in temporally gated SSN. Correlations with phoneme identification measures were also generally higher for pitch perception measures that included amplitude and frequency roving.

Correlations with phoneme identification measures were generally higher for complex tone discrimination measures than for pure tone discrimination measures. On average, cochlear implant users had 5.3 dB of masking release for consonants and 8.4 dB of masking release for vowels when measured in temporally gated SSN compared to stationary SSN. Cochlear implant pure tone frequency discrimination thresholds ranged between 1.5 and 9.9 %, while cochlear implant complex tone F0 discrimination thresholds ranged between 2.6 and 28.5 %. Phoneme identification was measured using consonant and vowel materials in quiet, in stationary speech-shaped noise (SSN), in spectrally notched SSN, and in temporally gated SSN. The effects of amplitude and frequency roving were measured under the rationale that individuals who are robust to such perturbations would perform better on phoneme perception measures. Complex tone fundamental frequency (F0) discrimination thresholds were measured for F0s of 110, 220, and 440 Hz. Pure tone frequency discrimination thresholds were measured for frequencies of 500, 1000, and 2000 Hz. This study examined correlations between pitch and phoneme perception for nine cochlear implant users and nine normal hearing listeners. Simulations with the point-biserial correlation coefficient show that for ρph ≠ 0, valid confidence intervals can be achieved with the iterated bootstrap only with medium or large sample sizes, depending on the distribution, while the standard method fails even then. Simulation results with the iterated bootstrap will be shown, which clearly demonstrate the ability of this bootstrap method to induce valid confidence intervals under all of the above mentioned conditions not only for ρ, but also for the difference of two correlation coefficients and the squared correlation coefficient. Some of the authors call into question the ability of any bootstrap methods of valid confidence intervals or acceptance regions for testing hypotheses about ρ under these conditions.
The overall result was that with non-normal (especially skewed) data, ρ ≠ 0 and small and medium sample sizes, bootstrap methods show poor coverage accuracy. Is distributed as Mann–Whitney U with sample sizes n 1 and n 0 when the null hypothesis is true.Several articles in the field of psychology have shown simulation results with the bootstrap-percentile method and variants for the (Pearson) correlation coefficient. If we divide the data set into two groups, group 1 which received the value "1" on Y and group 2 which received the value "0" on Y, then the point-biserial correlation coefficient is calculated as follows: To calculate r pb, assume that the dichotomous variable Y has the two values 0 and 1. This can be shown by assigning two distinct numerical values to the dichotomous variable.

The point-biserial correlation is mathematically equivalent to the Pearson (product moment) correlation that is, if we have one continuously measured variable X and a dichotomous variable Y, r XY = r pb. If this is the case, a biserial correlation would be the more appropriate calculation. When a new variable is artificially dichotomized the new dichotomous variable may be conceptualized as having an underlying continuity. In most situations it is not advisable to dichotomize variables artificially. Y) is dichotomous Y can either be "naturally" dichotomous, like whether a coin lands heads or tails, or an artificially dichotomized variable. The point biserial correlation coefficient ( r pb) is a correlation coefficient used when one variable (e.g.


 0 kommentar(er)
0 kommentar(er)
